Books
Armin Wachter
 Independently Published
Independently Published
ISBN: 9798336249552
1. Auflage: September 2024
Hard Cover, 464 Seiten

Leistungsanalyse von IT-Systemen
 Independently Published
Independently PublishedISBN: 9798336249552
1. Auflage: September 2024
Hard Cover, 464 Seiten

Beschreibung
Das vorliegende Lehr- und Übungsbuch behandelt die Leistungsanalyse von IT-Systemen mittels der operationalen Warteschlangentheorie und Performancetests. Es richtet sich hauptsächlich an Systemarchitekten und Systemanalysten, die mit der Planung, Messung, Bewertung oder Prognose des Leistungsverhaltens von IT-Systemen befasst sind. Darüber hinaus wird das Buch auch all jene begeistern, die sich ganz allgemein über praxisnahe Konzepte der IT-systemischen Leistungsanalyse informieren möchten.Die operationale Warteschlangentheorie ist eine vergleichsweise einfache und mathematisch intuitive Art der Modellierung von IT-Systemen. Die damit verbundenen Voraussetzungen und Leistungsgrößen sind praxisnah und können im Prinzip mit beliebiger Genauigkeit geprüft bzw. gemessen werden. Drei wichtige Fragen, die im Rahmen dieser Theorie adressiert werden, lauten:
- Durch welche Faktoren wird die Systemleistung beeinflusst?
- Wie hängt die Systemleistung konkret von diesen Faktoren ab?
- Wie lässt sich die Systemleistung prognostizieren und optimieren?
Performancetests sind physikalische Experimente, in denen ein IT-System künstlich unter Last gesetzt wird und die diesbezüglichen Systemreaktionen gemessen werden. Sie kommen beispielsweise zum Einsatz, wenn es um den direkten IT-systemischen Leistungsvergleich oder um die Parametrisierung/Validierung von IT-Systemmodellen geht. Aus messdatenanalytischer Sicht ist vor allem zu berücksichtigen, dass Performancetests immer auch zufälligen Einflüssen unterliegen. Deshalb ist es angebracht, die mit einem Performancetest verbundenen Messvorgänge als stochastische Prozesse und die aus den Messvorgängen resultierenden Messreihen als Prozessrealisierungen aufzufassen, die es mit Hilfe der induktiven Statistik hinsichtlich der relevanten prozessspezifischen Verteilungsparameter auszuwerten gilt.
Vorwort
Aus Nutzer- und Betreibersicht sind bei der Beurteilung der IT-Systemleistung drei Leistungsmerkmale besonders wichtig, nämlich Antwortzeit, Durchsatz und Auslastung. Die Antwortzeit beschreibt, wie schnell eine Anfrage vom System beantwortet wird. Der Durchsatz gibt an, wieviele Antworten pro Zeiteinheit vom System gesendet werden. Die Auslastung bemisst den Zeitanteil, in welchem das System aufgrund von Anfragen überhaupt beansprucht wird. Während Nutzer vornehmlich an kurzen Antwortzeiten interessiert sind, stehen für Betreiber in der Regel hohe Durchsätze und hohe Auslastungen bei gleichzeitig niedrigen Anschaffungs- und Betriebskosten im Vordergrund. Dies alles zu gewährleisten ist aus vielerlei Gründen nicht einfach, zum Beispiel weil kurze Antwortzeiten und hohe Auslastungen in einem natürlichen Spannungsverhältnis stehen.Vor diesem Hintergrund beschäftigt sich die Leistungsanalyse von IT-Systemen hauptsächlich mit Fragen der folgenden Art:
- Durch welche Faktoren wird die Systemleistung beeinflusst?
- Wie hängt die Systemleistung konkret von diesen Faktoren ab?
- Wie lässt sich die Systemleistung prognostizieren und optimieren?
Am Anfang einer jeden IT-systemischen Leistungsanalyse steht die Systemmodellierung. Hierbei wird das betreffende System in ein abstraktes und vereinfachendes Abbild seiner selbst, also in ein Modell überführt, wobei von allen Systemdetails abgesehen wird, die auf der angestrebten Betrachtungsebene für die Systemleistung irrelevant sind. Die Güte oder Validität des Modells bemisst sich danach, inwiefern es in der Lage ist, das Leistungsverhalten des Systems zu reproduzieren. Grundlage hierfür sind dedizierte Experimente am System, deren Rahmenbedingungen als Modellinput dienen und deren Messresultate mit dem Modelloutput verglichen werden. Mit zunehmender Zahl von erfolgreichen Modell-Experiment-Vergleichen wächst das Vertrauen, die relevanten systemischen Leistungsaspekte im Modell adäquat berücksichtigt zu haben. Mit einem auf diese Weise validierten Modell steht am Ende ein mächtiges Werkzeug zur Verfügung, mit dessen Hilfe sich das systemische Leistungsverhalten unter den verschiedensten Rahmenbedingungen vorhersagen lässt.
Die prominentesten Vertreter von IT-Systemmodellen sind Warteschlangenmodelle. In ihnen wird ein IT-System als ein Netzwerk von Stationen dargestellt, die von einzelnen Jobs in unterschiedlicher Weise durchlaufen werden. Jede Station umfasst einen Wartebereich, in welchem Jobs auf Verarbeitung warten, und einen Bedienbereich mit ein oder mehreren Prozessoren, wo die eigentliche Jobverarbeitung stattfindet (siehe Abbildung 1).
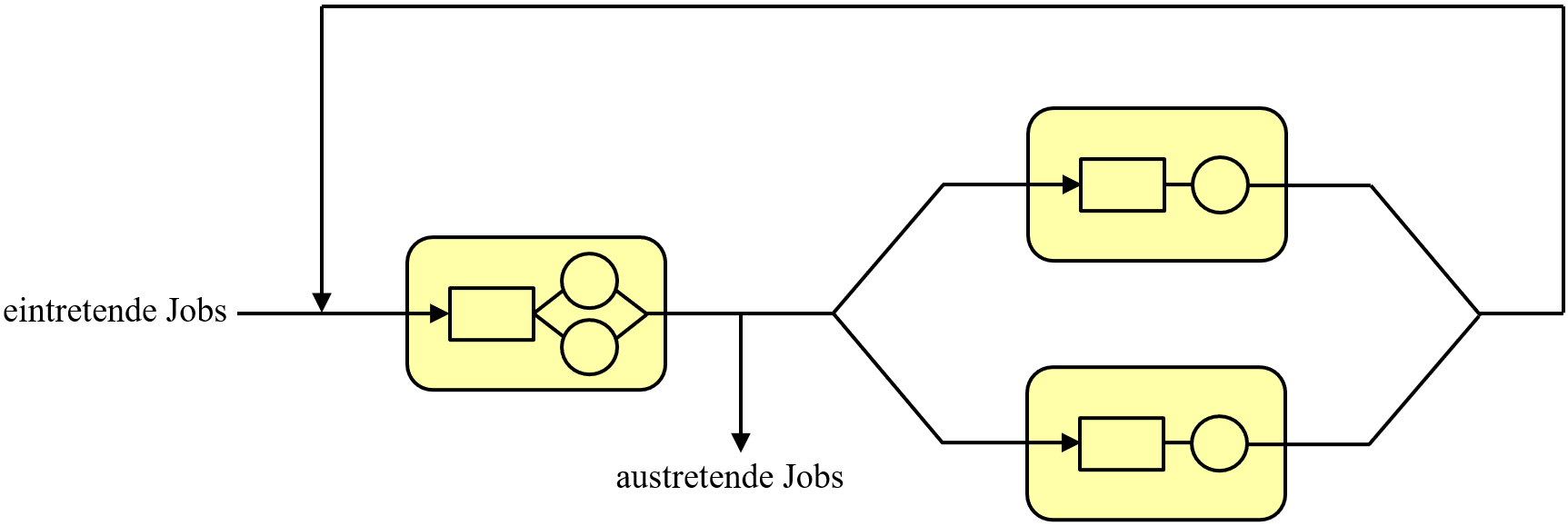
Abbildung 1. Netzwerk eines Warteschlangenmodells. In diesem Beispiel umfasst das Netzwerk einen Jobeingangs- und einen Jobausgangskanal, eine Zweiprozessorstation und zwei parallel geschaltete Einprozessorstationen. Die Rechtecke repräsentieren Wartebereiche, und die Kreise stehen für Prozessoren. Die Pfeile zeigen die Laufrichtung der Jobs durch das Netzwerk an. Ein Netzwerk heißt geschlossen, wenn in ihm eine feste Zahl von Jobs zirkuliert. Ansonsten ist es offen (so wie hier). Geschlossene Netzwerke eignen sich zur Modellierung von Batchsystemen oder von Systemen mit einer festen Zahl von aktiven Nutzern. Bei allen anderen Systemen sind offene oder gemischte Netzwerke zu bevorzugen.
Wie sich zeigt, besitzen Warteschlangenmodelle einen geeigneten Abstraktionsgrad, um die Leistung von IT-Systemen in Form von Antwortzeiten, Durchsätzen, Auslastungen und weiteren "makroskopischen" Leistungsmerkmalen effizient studieren zu können. Warteschlangenmodelle lassen sich hauptsächlich in drei Kategorien unterteilen:
(1) Stochastische Warteschlangenmodelle. Hierbei werden die meisten Modellfreiheitsgrade als Zufallsvariablen definiert. Der modellhafte Netzwerkbetrieb besteht deshalb im wesentlichen aus stochastischen Prozessen (also aus zeitlich geordneten Folgen von Zufallsvariablen), die sich unter sehr speziellen Bedingungen in mathematisch geschlossener Form ausarbeiten lassen. Infolgedessen sind natürlich auch die resultierenden Leistungsmerkmale größtenteils stochastischer Natur. Die Wurzeln der stochastischen Warteschlangentheorie reichen zurück bis zum Anfang des zwanzigsten Jahrhunderts, als sich der dänische Mathematiker Agner Krarup Erlang mit Wartezeitproblemen bei der zentralen Vermittlung von Telefongesprächen beschäftigte. Spätestens seit den 1960er Jahren gehört diese umfangreiche, mathematisch anspruchsvolle und auch heute noch nicht abgeschlossene Theorie zu den Standardwerkzeugen der IT-systemischen Leistungsanalyse.
(2) Simulative Warteschlangenmodelle. Ihnen liegt die Idee zugrunde, konkrete Ausprägungen der modellhaften Netzwerkdynamik im Detail nachzustellen. In der besonderen Form der diskreten Ereignissimulation wird die Reise eines jeden Jobs durch das Netzwerk mit Hilfe eines Computerprogramms und auf der Basis eines wohldefinierten (pseudozufälligen oder deterministischen) Regelwerkes akkurat verfolgt und an den Ereigniszeitpunkten, zum Beispiel wenn der Job eine Station betritt oder verlässt, protokolliert. Die Auswertung der protokollierten Daten geschieht in ähnlicher Weise wie bei Experimenten an realen Systemen. Ein Vorteil des simulativen Ansatzes ist, dass er im Prinzip keinen Einschränkungen bezüglich der Implementierung von speziellen Netzwerkfunktionalitäten unterworfen ist. Deshalb lassen sich hiermit auch Systeme analysieren, die anderen Analysemethoden nicht zugänglich sind. Dem steht allerdings der Nachteil gegenüber, dass die Entwicklung und Durchführung von Simulationen oftmals sehr aufwändig ist.
(3) Operationale Warteschlangenmodelle. Wie stochastische Modelle besitzen sie einen geschlossenen mathematischen Formalismus. Allerdings werden die modellhaften Voraussetzungen und Leistungsgrößen nicht stochastisch sondern operational definiert, mit der Bedeutung, dass sie auf einen festen Zeitraum bezogen sind und in genau diesem Zeitraum am realen System geprüft bzw. gemessen werden können. Entscheidend hierbei ist nicht, dass die Prüfungen und Messungen tatsächlich stattfinden, sondern dass sie prinzipiell möglich sind. Um dies zu verdeutlichen, betrachte man einen Webserver, dessen modellhaftes Netzwerk aus einer einzigen Station mit einem Jobeintritts- und einem Jobaustrittskanal besteht. Im Rahmen der stochastischen Theorie bestünde eine typische Modellvoraussetzung darin, dass die Zwischeneintrittszeiten der Jobs unabhängig und identisch exponentialverteilt sind. Diese Voraussetzung lässt sich schon allein aufgrund der Bedeutung des Begriffes "Zufallsvariable" weder exakt noch ungefähr am Webserver prüfen; sie ist daher nicht operational. Im Rahmen der operationalen Theorie könnte man dagegen annehmen, dass in einem bestimmten Zeitraum die stationsseitigen Jobeintritts- und Jobaustrittszahlen übereinstimmen. Diese Voraussetzung ist in der Tat operational, weil man sie am Webserver einfach durch Zählung der eingehenden Anfragen und gesendeten Antworten im besagten Zeitraum exakt prüfen kann.
Die operationale Warteschlangentheorie wurde von Peter J. Denning, Jeffrey P. Buzen und anderen Informatikern Mitte der 1970er Jahre eingeführt und kann als eine Reaktion auf folgende Beobachtungen im praktischen Umgang mit der stochastischen Theorie aufgefasst werden:
- Stochastische Voraussetzungen sind ihrem Wesen nach grundsätzlich nicht experimentell verifizierbar (wie soeben diskutiert). Infolgedessen kann ein stochastisches Warteschlangenmodell streng genommen nicht validiert werden.
- Stochastische Modelle sind in der Lage, das Leistungsverhalten vieler IT-Systeme mit erstaunlicher Genauigkeit vorherzusagen, und zwar auch dann, wenn die Systeme einige Modellvoraussetzungen mit ziemlicher Sicherheit nicht erfüllen. Demnach scheinen stochastische Modelle über "versteckte Merkmale" zu verfügen, die die eigentlichen Ursachen des Erfolges sind.
- Ein Systemanalyst, der mit konkreten praktischen Leistungsfragen konfrontiert ist, tut sich in der Regel schwer, diese in einem stochastischen Kontext zu sehen und zu bearbeiten.
Gegenüber der stochastischen Theorie zeichnet sich die operationale Theorie vor allem durch drei Eigenschaften aus:
- Die stochastische Theorie macht Aussagen über alle möglichen konkreten Ausprägungen der Netzwerkdynamik, die mit den gegebenen Voraussetzungen im Einklang stehen, und zwar in Form von Wahrscheinlichkeitsverteilungen, Erwartungswerten, Varianzen und ähnlichem (Man kann sich eine konkrete Ausprägung der Netzwerkdynamik als eine Netzwerksimulation mit bestimmten Anfangsbedingungen und einer bestimmten Initialisierung des Pseudo-Zufallszahlengenerators vorstellen). In der operationalen Theorie können dagegen alle voraussetzungskonformen netzwerkdynamischen Ausprägungen als operational identisch betrachtet werden. Es genügt daher, sich gedanklich auf irgendeine dieser Ausprägungen zu beschränken und diese eine mit Hilfe von einfachen Mittelwerten über den definierten Messzeitraum zu beschreiben.
- Dieser fundamentale Unterschied bedeutet, dass die operationalen Leistungsgrößen einen anderen und auch geringeren Informationsgehalt besitzen als die stochastischen. Dafür bietet die operationale Theorie einen intuitiveren und mathematisch einfacheren Formalismus, der vor allem dem Praktiker entgegenkommt.
- Erstaunlicherweise ist die operationale Theorie trotzdem in der Lage, viele zentrale Gesetzmäßigkeiten der stochastischen Theorie zu reproduzieren, natürlich vorbehaltlich der damit verbundenen Interpretationsunterschiede. Beispiele hierfür sind das Littlesche Gesetz, die Ankunftstheoreme sowie die Produktformlösungen für separable Netzwerke.
Performancetests. Grundsätzlich ist man bei jeder Art der IT-systemischen Leistungsevaluierung immer auch auf Leistungsmessungen von realen IT-Systemen angewiesen. Hierzu kommen in der Regel Performancetests zum Einsatz, in denen jeweils ein bestimmtes System in offener oder geschlossener Form über einen längeren Zeitraum hinweg künstlich unter Last gesetzt wird und die diesbezüglichen Systemreaktionen (Antwortzeiten, Durchsätze, Auslastungen etc.) fortlaufend gemessen werden. Fokussiert man sich hierbei auf die messdatenanalytischen Aspekte, so sind vor allem folgende Punkte hervorzuheben:
- Jeder Performancetest ist zwangsläufig unkontrollierbaren und unvorhersehbaren Einflüssen ausgesetzt. Deshalb ist es angebracht, (i) den Test als ein dynamisches Zufallsexperiment, (ii) die mit dem Test verbundenen Messvorgänge als stochastische Leistungsprozesse (also als zeitlich geordnete Folgen von Zufallsvariablen) und (iii) die aus den Messvorgängen resultierenden Messreihen als konkrete Realisierungen der Prozesse aufzufassen.
- Demzufolge besteht die Hauptaufgabe der Messdatenanalyse darin, die interessierenden Verteilungsparameter (Erwartungswerte, Varianzen etc.) eines jeden Leistungsprozesses anhand der vorliegenden, in ein oder mehreren Testwiederholungen generierten Prozessrealisierungen möglichst akkurat zu schätzen (induktive oder inferenzielle Statistik).
- Die hierfür zur Verfügung stehenden statistischen Analysemethoden adressieren unterschiedliche Interessenschwerpunkte und beruhen größtenteils auf der Strategie, das jeweilige Schätzproblem auf ein Standardproblem der statistischen Schätztheorie zurückzuführen (siehe Abbildung 2).
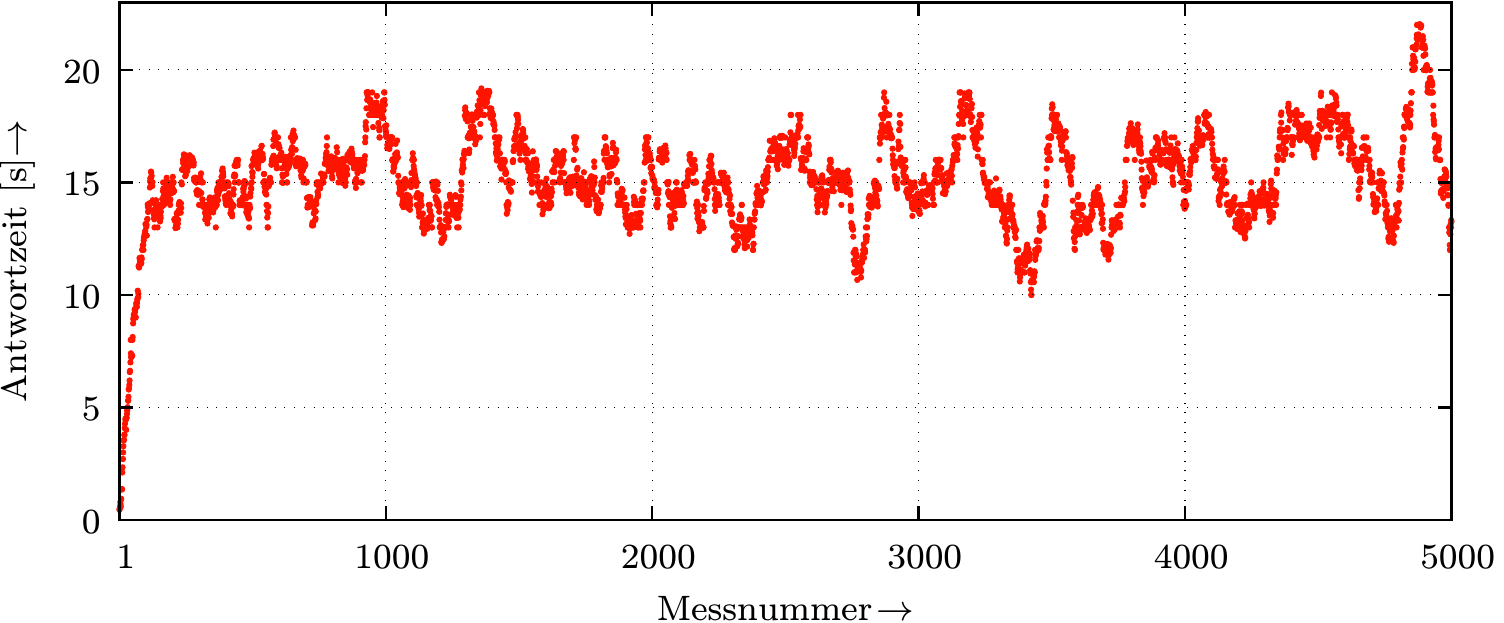
Abbildung 2. Gemessene Antwortzeiten eines Webservers im Rahmen eines geschlossenen Performancetests mit konstantem Lastprofil. Aus der stochastischen Perspektive entspricht die Messreihe einer konkreten Realisierung des abstrakten serverseitigen Antwortzeitprozesses. Offensichtlich oszillieren die Messwerte wellenförmig, und zwar dergestalt, dass auf einen kleinen (großen) Wert ein ähnlich kleiner (großer) Wert folgt. Dies deutet darauf hin, dass testzeitlich eng benachbarte Prozessvariablen positiv korreliert sind. Ferner erkennt man anhand der linken Messwerte, dass der Prozess eine gewisse Zeit benötigt, um sich "einzuschwingen". Möchte man den stationären (langfristigen) Prozesserwartungswert allein auf der Basis dieser einen Prozessrealisierung bestimmen, so kann man hierfür die statistische Schätztheorie nicht direkt in Anschlag bringen, weil die einzelnen Prozessvariablen (i) nicht unabhängig voneinander und (ii) in der Einschwingphase nicht identisch verteilt sind. Deshalb böte es sich hier an, die Messreihe dergestalt zu transformieren, dass sie als Realisierung eines anderen Prozesses aufgefasst werden kann, der seinerseits in guter Näherung aus einer Folge von unabhängigen und identisch verteilten Zufallsvariablen besteht und darüber hinaus den gesuchten Erwartungswert besitzt. Notwendige Voraussetzung hierfür ist allerdings, dass der ursprüngliche Antwortzeitprozess ergodisch ist und somit seinen momentanen Zustand hinreichend schnell vergisst.
Buchinhalte. Das vorliegende Buch behandelt die Leistungsanalyse von IT-Systemen mittels der operationalen Warteschlangentheorie und Performancetests. Es richtet sich an Systemarchitekten und Systemanalysten, die mit der Planung, Messung, Bewertung oder Prognose des Leistungsverhaltens von IT-Systemen befasst sind. Eine weitere Zielgruppe sind Dozenten und Studenten der theoretischen Informatik. Für sie liefert das Buch eine gedankliche Basis, auf die viele Konzepte und Resultate der stochastischen Warteschlangentheorie heruntergebrochen werden können, um auf diese Weise ein intuitiveres Verständnis der Materie zu generieren. Schließlich können auch all jene von dem Buch profitieren, die sich ganz allgemein über praxisnahe Konzepte der IT-systemischen Leistungsanalyse informieren möchten.
Das Buch ist in vier Kapitel und zwei Anhänge unterteilt. Das erste Kapitel beschäftigt sich mit den Grundzügen der operationalen Warteschlangentheorie. Hierzu gehören die Beschreibung des operationalen Basismodells, die Entwicklung der wichtigsten Leistungsgrößen und allgemeinsten Gesetze sowie die konzeptionelle Erweiterung der Theorie in Form der sogenannten homogenen Netzwerke. Sie zeichnen sich dadurch aus, dass das Verhalten einer jeden Station ausschließlich von ihrer eigenen momentanen Besetzung mit Jobs abhängt. In diesem Zusammenhang werden auch die Begriffe Zustand, Zustandsübergang und Zustandsverteilung (in einem nicht-stochastischen Sinne) eingeführt, die für die exakte Bestimmung des netzwerkseitigen Leistungsverhaltens im dritten Kapitel von zentraler Bedeutung sind.
Im zweiten Kapitel stellen wir die wichtigsten Analysetechniken für geschlossene homogene Netzwerke vor, bei denen auf die Kenntnis der Zustandsverteilung verzichtet werden kann. Dementsprechend handelt es sich hierbei vornehmlich um Eingrenzungs- und Approximationstechniken. Ihr Vorteil besteht darin, dass sie schnell und mit leichter Hand zum Einsatz gebracht werden können und trotzdem Vorhersagen liefern, die in vielen Anwendungsfällen hinreichend genau sind.
Das dritte Kapitel handelt von der exakten Leistungsberechnung von offenen und geschlossenen homogenen Netzwerken. Dies läuft im wesentlichen auf das Lösen von linearen Gleichungssystemen für die Zustandsverteilung hinaus. Das besondere an den Lösungen ist, dass sie sich aus den Lösungen der einzelnen, in Isolation betrachteten Stationen multiplikativ zusammensetzen (Produktformlösungen). Weil die Auswertung der Lösung im geschlossenen Fall recht komplex ist, beschäftigen sich gleich mehrere Abschnitte damit.
Das vierte Kapitel ist der Konzeption und statistischen Analyse von Performancetests gewidmet, wobei wir uns auf solche Tests beschränken, bei denen die quantitative Bestimmung von IT-systemischen Leistungsgrößen — etwa im Kontext des direkten Leistungsvergleiches von IT-Systemen oder der Parametrisierung/Validierung von IT-Systemmodellen — im Vordergrund steht. Das vorrangige Ziel des Kapitels ist die Erarbeitung von einfachen und praktikablen Methoden zur statistischen Schätzung von bestimmten Verteilungsparametern der mit einem Performancetest verbundenen Leistungsprozesse. Auf dem Weg dorthin wird es sich als hilfreich erweisen, zunächst den stochastischen Charakter von Performancetests herauszuarbeiten und anschließend einige Bereiche der statistischen Schätztheorie zu diskutieren.
Im ersten Anhang werden schließlich die wahrscheinlichkeitstheoretischen Grundlagen bereitgestellt, die im vierten Kapitel benötigt werden.
Das Buch ist als Lehr- und Übungsbuch konzipiert. Wichtige Voraussetzungen und Beziehungen sind in Definitions- und Satzkästen zusammengefasst, um so dem Leser ein strukturiertes Lernen und schnelles Nachschlagen zu ermöglichen. Desweiteren befindet sich am Ende eines jeden Kapitels eine Zusammenfassung, gefolgt von vielen Aufgaben mit Lösungen, mittels derer das Verständnis des behandelten Stoffes überprüft werden kann. Einige der insgesamt 130 Aufgaben gehen auch über den Lehrstoff hinaus. Die ersten drei Kapitel bewegen sich mathematisch auf niedrigem Niveau und setzen lediglich Kenntnisse in linearer Algebra und Kombinatorik voraus. Für das Verständnis des vierten Kapitels und des ersten Anhangs sind zusätzlich Kenntnisse der Differential- und Integralrechnung notwendig.
Dieses Buch erhebt keinen Anspruch auf Vollständigkeit. Stattdessen wurden seine Inhalte so ausgewählt, dass sie einerseits die grundlegenden Konzepte der operationalen Warteschlangentheorie sowie der statistischen Analyse von Performancetests enthalten und andererseits den Bedürfnissen des Praktikers — die Anwendung dieser Theorien auf konkrete IT-systemische Leistungsfragen — gerecht werden. Auf der Grundlage des hier präsentierten Stoffes sollte der Leser in der Lage sein, sich weitere Themen selbstständig zu erarbeiten. Auch hierzu sind die kommentierten Literaturvorschläge im zweiten Anhang hilfreich.
Köln im August 2024
Armin Wachter



